A small idea before the fireworks show

Thoralf Skolem was a mathematician who worked in mathematical logic, set theory, and number theory. He was the only known PhD student of Axel Thue, whose
Thue systems were an early word-based model of computation. Skolem had only one PhD student, Öystein Ore, who did not work in logic or computation. Ore did, however, have many students including Grace Hopper and Marshall Hall, Jr., and Hall had many more including Don Knuth.
Today Ken and I try to stimulate progress on a special case of Skolem’s problem on linear sequences.
Although Ore worked mainly on ring theory and graph theory the seeds still collected around Skolem’s tree: Hall’s dissertation was titled “An Isomorphism Between Linear Recurring Sequences and Algebraic Rings.” Sequences defined by a finite linear operator are about the simplest computational process we can imagine:
The coefficients

and initial values

can be integers or relaxed to be algebraic numbers. Skolem posed the
problem of deciding whether there is ever an
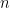
such that
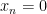
.
This is a kind of halting problem. It seems like it should be simple to analyze—it is just linear algebra—but it has remained open for over 80 years. We have
discussed it
several times
before. This 2012
survey by Joel Ouaknine and James Worrell, plus this
new one, give background on this and some related problems.
The Sum-of-Powers Case
Let
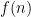
be
where each
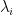
is an algebraic integer. Our problem is:
Does there exist a natural number 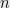 so that
so that  ?
?
This is a special case of the Skolem problem. It arises when the coefficients

are the evaluations of the elementary symmetric polynomials

at

with alternating signs. For example, with
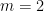
we get
which for
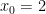
and

gives
and so on. For
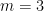
we have
Then
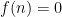
means
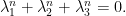
If the

are nonzero integers then for odd
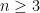
this is asking whether
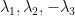
is a solution to Pierre Fermat’s equation, and we can simply answer “no.” Of course whether

is a solution can be easier than asking whether the equation has a solution, but this shows our case contains some of the flavor of Fermat’s Last Theorem.
We can point up some minor progress on this problem. Our methods can handle somewhat more general cases where the sum of
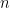
-th powers is multiplied by
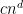
for some fixed constants

and

, but we will stay with the simpler case. Our larger hope is that this case embodies the core of the difficulty in Skolem’s problem, so that solving it might throw open the road to the full solution.
Proof
Let’s begin the proof for the case when
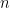
is a prime

. Suppose that
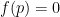
. Recall
Clearly we can assume that
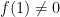
. Note that this is decidable. Put
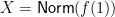
. The key is to look at the quantity
where

is a prime. We employ the following generalization of the binomial theorem:
where
The upshot is that all terms are divisible by a proper factor of
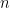
except those from the cases
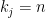
, all other
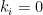
. Each gives a factor of

and leaves the term

. When
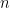
is a prime

this factor must include

itself. Thus we get that

for some
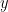
of the form
where

is an algebraic integer. But by the supposition
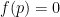
this simplifies to

, and so
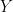
is divisible by

. Thus
Since
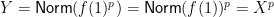
,

too is divisible by

. But

is independent of
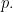
Hence,

acts as a bound on any possible prime

such that
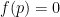
. Testing the finitely many values of

up to

thus yields a decision procedure for this restricted case of Skolem’s problem.
Fine-Tuning and Fireworks
Ken chimes in an observation that might be distantly related: The Vandermonde determinant
is the “smallest” alternating polynomial in
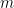
variables. Together with the symmetric polynomials it generates all alternating polynomials. When the
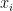
are the
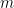
-th roots of unity it gives the determinant of the Fourier matrix
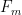
up to sign. This determinant has absolute value
It is also the product of the lengths of the

chords formed by
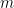
equally-spaced points on the unit circle. The observation is that this 2-to-the-nearly-linear quantity is extraordinarily finely tuned.
To see how, let’s estimate the product of the chords in what is caricatured as the style of physicists: The length of an average chord is
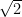
. So we can estimate the size of the product as
This is off by an order of magnitude
in the exponent—not even close. We can be a little smarter and use the average length of a chord instead, integrating
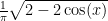
from
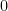
to

to get
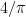
. This is still a number greater than
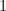
and plugs in to yield
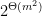
anyway.
Such a calculation looks silly but isn’t. If we enlarge the circle by a factor of

then every term in the product is multiplied by that factor and it dominates:
If we shrink the circle by
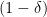
the opposite happens: we divide by
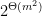
which crushes everything to make the analogous quantity
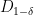
virtually zero. Furthermore this “big crush” happens under more-plausible slight perturbations such as forbidding any of the
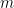
points from occupying the arc between
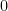
and

radians, which prevents the equal-spacing maximization when

. We
covered this at length in 2011.
The underlying reality is that when you take the logarithm of the product of chords, the terms of all growth orders between

and

all magically cancel. There are many more chords of length

than chords of length

, but the latter can be unboundedly short in a way that perfectly balances the multitudes of longer chords. The actual value of
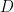
seems tiny amidst these perturbative possibilities.
This gigantic cancellation reminds Dick and me of the present argument over the tiny observed magnitude of the
cosmological constant 
. Estimation via quantum field theory prescribes a value 120 orders of magnitude higher—one that would instantly cause our universe to explode in fireworks—unless vast numbers of terms exactly cancel. Quoting Wikipedia:
This discrepancy has been called “the worst theoretical prediction in the history of physics” … the cosmological constant problem [is] the worst problem of fine-tuning in physics: there is no known natural way to derive the tiny [value] from particle physics.
“Fine-tuning” of constants without explanation is anathema to science, and many scientists have signed onto theories that there is a multiverse with 500 or more orders of magnitude of universes, enough to generate some with the tiny

needed to allow life as we know it. However, any fine-tuning discovered in mathematics cannot be anathema. Perhaps the universe picks up the Fourier fine balancing act in ways we do not yet understand. More prosaically, the fine balance in quantities similar to
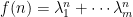
above could be just what makes Skolem’s problem hard.
Open Problems
I believe that the general case of the Skolem can be handled, not just the simple case. But the problem of handling more than just primes seems hard. I believe that this method can be used to handle more cases than just primes. Ken and I are working on this. Meanwhile, we wish everyone Stateside a happy Fourth of July, whether or not that includes fireworks.
Source URL: https://rjlipton.wordpress.com/2015/07/04/the-halting-problem-for-linear-machines/

so that
?
0 comments:
Post a Comment